本文的主要目的是尽量简单地解释 [Bu, Halpern-Leistner, Ibáñez Núñez, Kinjo] 中定义的组合晶格. 这种结构使得 Lie 理论中的很多有用的概念可以推广到叠理论中, 例如特征、余特征、根系、Weyl 群等.
虽然上述文章写得有些技术性, 但其中的一些直观思想并不那么困难, 本文就是为了解释这些思想. 本文的前置知识包括基本的范畴论及对复 Lie 群较好的了解.
目录
Lie 理论复习§
Lie 理论中与本文有关的部分, 也是数学中我觉得最美的部分之一, 是复 Lie 群与 Euclid 空间中具有完美对称性的图案⸺根系⸺之间的对应关系.
例如, Lie 群 $\mathrm{GL}_3 (\mathbb{C})$ 对应于 $\mathbb{R}^3$ 中的如下根系:

这里, 我们沿 $(1, 1, 1)$ 方向将 $\mathbb{R}^3$ 投影到平面上, 这样能更好地从图中看到根系的对称性. 图中的 $6$ 个蓝色点表示 $6$ 个根, 其坐标为 $(1, -1, 0)$ 及其置换, 均落在平面 $x + y + z = 0$ 上. 蓝色直线表示垂直于根向量的平面, 分别由 $x = y$, $y = z$, $x = z$ 定义. 浅蓝色区域由不等式 $x \geq y \geq z$ 给出, 它是由这些平面切出的一个胞腔, 图中共有 $6$ 个胞腔.
这个构造对一般的复 Lie 群 $G$ 大致是这样的: 复 Lie 群 $G$ 有极大环面 $T \subset G$, 它形如 $T \simeq (\mathbb{C}^\times)^n$, 其中 $\mathbb{C}^\times = \mathbb{C} \setminus \{ 0 \}$ 是非零复数的乘法群. 自然数 $n$ 称为 $G$ 的秩. 例如, $\mathrm{GL}_n (\mathbb{C})$ 的秩就是 $n$, 其中由对角阵构成的子群是 $G$ 的一个极大环面.
我们考虑 $T$ 的余特征晶格和特征晶格, $$ \begin{aligned} \Lambda_T & = \mathrm{Hom} (\mathbb{C}^\times, T) \simeq \mathbb{Z}^n \ , \\[1ex] \Lambda^T & = \mathrm{Hom} (T, \mathbb{C}^\times) \simeq \mathbb{Z}^n \ , \end{aligned} $$ 它们互为对偶. 有时, 我们也考虑实向量空间的版本 $\Lambda_T \otimes \mathbb{R} \simeq \mathbb{R}^n$ 和 $\Lambda^T \otimes \mathbb{R} \simeq \mathbb{R}^n$.
$G$ 的根的集合 $\Phi \subset \Lambda_T$ 是如下定义的有限集: 将 $G$ 的 Lie 代数 $\mathfrak{g}$ 通过 $T$ 的共轭作用视为 $T$ 的表示, 则 $\Phi \subset \Lambda^T$ 就是这个表示中出现的非零权的集合. 每个根也对应 $\Lambda_T$ 中一个超平面, 这些超平面的集合称为 $\Lambda_T$ 中的根超平面排布, 也就是图 1 中的蓝线.
根的集合常常具有 “完美的对称性”, 即构成根系. 若具有这种对称性, 则 $G$ 称为约化群. 例如, $\mathrm{GL}_n (\mathbb{C})$ 是约化群.
$G$ 的 Weyl 群 $W$ 是一个有限群, 它能够作用于 $\Lambda_T$ 和 $\Lambda^T$, 定义为 $W = \mathrm{N}_G (T) / \mathrm{Z}_G (T)$. 若 $G$ 是连通约化群, 则 $W$ 正是所有关于根超平面的反射构成的群. 例如, $\mathrm{GL}_n (\mathbb{C})$ 的 Weyl 群是置换群 $\mathrm{S}_n$, 其作用于 $\Lambda_T$ 就是置换 $n$ 个坐标, 图 1 中也是如此.
本文中, 我们特别关注商集 $$ \Lambda_T / W \quad \text{与} \quad \Lambda^T / W \ , $$ 它们也能视为根超平面排布中的单个胞腔, 即图 1 中的浅蓝色区域. 这些商集在表示论中频繁出现, 虽然它们出现时不常像这样表述为商集. 例如, 当 $G$ 为约化群时, 有以下结论:
上同调: 分类空间 $\mathrm{B} G$ 的上同调是 $$ \mathrm{H}^\bullet (\mathrm{B} G; \mathbb{Q}) \simeq \mathbb{Q} [x_1, \dotsc, x_n]^W \ , $$ 其中 $x_1, \dotsc, x_n$ 是 $\Lambda_T$ 的一组坐标, 上标 $W$ 表示 Weyl 群作用下不变的部分. 换言之, 该上同调是 $\Lambda_T$ 上在 Weyl 群作用下不变的多项式的空间, 也即 $\Lambda_T / W$ 上多项式函数的空间.
表示: $G$ 的所有有限维表示都能分解为不可约表示的直和, 而这些不可约表示一一对应于 $\Lambda^T / W$, 其中每个表示对应于其最高权.
余特征: $G$ 的余特征的共轭类, 即同态 $\mathbb{C}^\times \to G$ 的共轭类, 一一对应于 $\Lambda_T / W$.
叠§
叠是一类非常有趣的几何对象, 在代数几何、微分几何、数论和物理中都有广泛应用. 正如流形在经典几何中不可或缺, 叠 (及其变体) 在描述现实世界的量子几何中也不可或缺.
对初学者而言, 叠可能看起来很难, 毕竟教科书 The Stacks project 已经写了 7000 多页. 但其背后的基本思想并没有看起来那么困难.
首先回忆, 群胚定义为所有态射均可逆的范畴. 这里, 我们略微不同地想象群胚: 我们将其想象成一个集合, 并给每个元素配上一个群, 称为其自同构群.
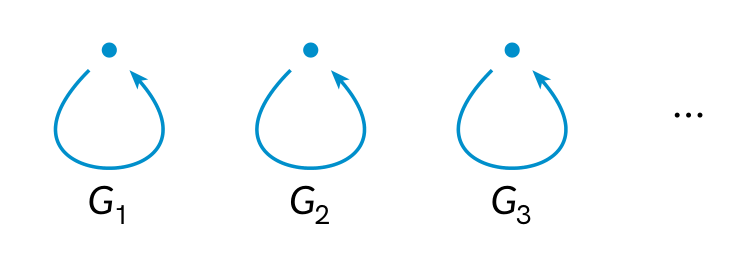
我们不难将这样的对象自然地视为群胚. 反过来, 也不难验证任何 (小) 群胚都等价于一个这样得到的群胚.
叠可以大概定义为 Lie 群胚, 即其中对象、态射的集合都是复流形的群胚. 换言之, 叠就像一个复流形, 但每个点都配有一个复 Lie 群, 作为其自同构群.
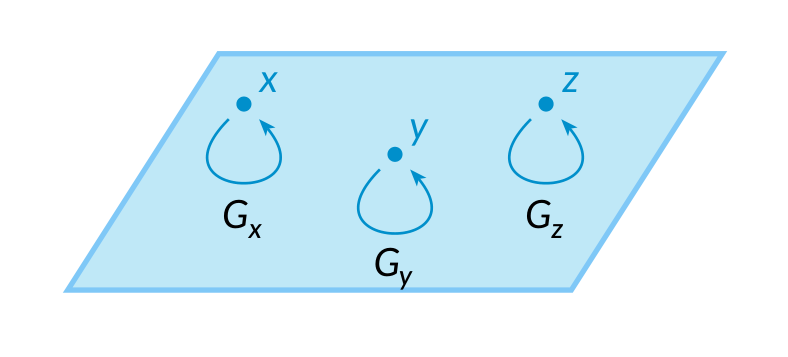
例如, 每个复流形自身都是一个叠, 其中每个点的自同构群都是平凡群.
一个不那么平凡的例子是, 对复 Lie 群 $G$, 有分类叠 $* / G$, 它只有一个点, 其自同构群是 $G$. 这样一来, Lie 群就可以视为叠的特例.
关于叠定义的注记
叠的准确定义比较复杂, 主要是因为叠之间的等价比较难以刻画: 即使两个叠各自的对象、态射的流形不同, 如果它们在某种意义上 “范畴等价”, 那么就也应该将它们视为同一个叠. 这使得定义叠之间的态射也变得复杂, 因为上述这种范畴等价需要具有逆态射而成为同构. 但只要处理好这一点, 就能得到叠的正确定义.
另一个问题是, 在实际应用中, 常常需要考虑不光滑的空间, 有时也需要使用代数簇或概形. 这也将叠的理论变得更复杂, 并导致需要各种关于 Grothendieck 拓扑的凌乱讨论, 但我们在此不考虑这一点.
对 $\mathbb{C}$ 上定义的叠 $X$, 有几何实现 $|X|$, 它是在相差同伦等价的意义下良好定义的拓扑空间. 例如, 分类叠 $* / G$ 的几何实现就是分类空间 $\mathrm{B} G$, 这也是单点空间 $*$ 关于 $G$ 的同伦商空间.
组合晶格§
正如上面解释, 叠可视为 Lie 群的推广. 相应地, 叠的组合晶格则是前面提到过的 Lie 群的组合对象 $\Lambda_T / W$ 的推广.
大致来说, 对叠 $X$, 其组合晶格 $\mathrm{CL} (X)$ 定义如下: 对每个点 $x \in X$, 取其自同构群 $G_x$, 再取该群的 $\Lambda_T / W$, 最后将这些不同的 $\Lambda_T / W$ 按照 $X$ 的拓扑粘起来.
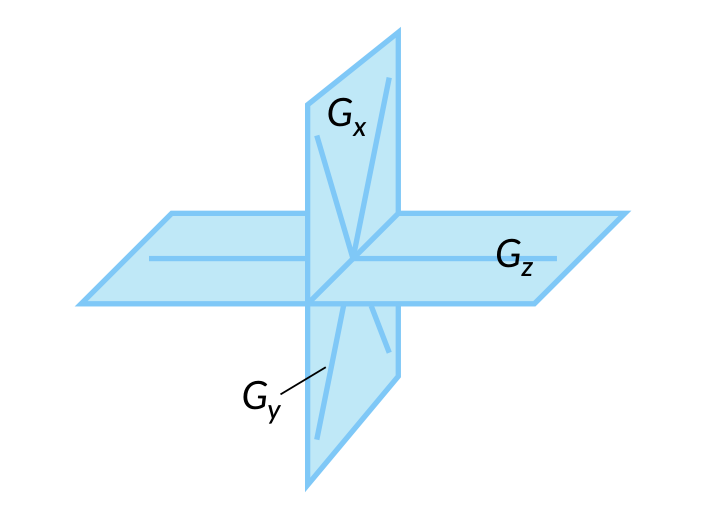
图中, 每个平面都应该除掉各自的 Weyl 群, 因此实际上应该只剩一个胞腔, 但我们还是将整个平面画了出来, 这样看得更清晰.
通常情况下, 只需用有限片 $\Lambda_T / W$ 来进行粘合, 因为其他的每片都包含在其中某一片中, 或者与其中一片完全重合, 正如图 4 中 $G_y$ 的那一片包含在 $G_x$ 的那一片中.
组合晶格的准确定义如下. 对 $\mathbb{C}$ 上的叠 $X$, 定义其组合晶格为 $$ \mathrm{CL} (X) = \text{π}_0 \bigl( \, \mathrm{Map} (* / \mathbb{C}^\times, X) \, \bigr) \ , $$ 即从 $* / \mathbb{C}^\times$ 到 $X$ 的所有映射构成的空间的连通分支的集合.
例如, 若 $X = * / G$ 是分类叠, 则 $* / \mathbb{C}^\times \to * / G$ 的映射也就是 $\mathbb{C}^\times \to G$ 的同态的共轭类, 与 $\Lambda_T / W$ 一一对应. 也就是说, $$ \mathrm{CL} (* / G) \simeq \Lambda_T / W \ . $$
对更一般的叠 $X$, 映射 $* / \mathbb{C}^\times \to X$ 其实就是一个点 $x \in X$ 再加上一个同态 $\mathbb{C}^\times \to G_x$ 的共轭类, 而取这些映射的空间的连通分支的集合则相当于说, 如果有两个这样的映射, 其中一个可以连续变换到另一个, 则将它们等同起来. 这就解释了为何 $\mathrm{CL} (X)$ 可以由 $X$ 中各个点处的 $\Lambda_T / W$ 粘起来得到.
应用§
Weyl 群§
通过组合晶格, 我们可以得到 Weyl 群向叠的推广. 在 [Bu, Halpern-Leistner, Ibáñez Núñez, Kinjo] 中, 对叠 $X$, 我们构造了一个称为特殊面范畴的范畴, 它通常是有限的, 而其中对象的自同构群具有类似 Weyl 群的性质.
例如, 对分类叠 $* / G$, 这个范畴的对象就是 Levi 子群 $L \subset G$, 而 $L$ 在该范畴中的自同构群则是相对 Weyl 群 $W_L = \mathrm{N}_G (\mathrm{Z} (L)) / \mathrm{Z}_G (\mathrm{Z} (L))$. 当 $L$ 极小时, 这就是 $G$ 的 Weyl 群.
根系§
我们至此还未提到根系的推广. 这样的推广在 [Bu, Halpern-Leistner, Ibáñez Núñez, Kinjo: §5.3] 中有所讨论, 其中 Lie 群的根推广为叠的余切权.
其他§
还有很多关于 $\Lambda_T / W$ 和 $\Lambda^T / W$ 的有用结果也能推广到叠, 包括所有在 §1 末尾列出的结果. 那里提到的关于余特征的结果已经作为组合晶格的定义, 而关于上同调、表示论的两个结果分别在 [Bu, Davison, Ibáñez Núñez, Kinjo, Pădurariu] 和 [Bu, Pădurariu, Toda] 中研究. 我相信更多类似的结果会在将来出现.
参考文献§
Bu, C., Davison, B., Ibáñez Núñez, A., Kinjo, T., and Pădurariu, T. Cohomology of symmetric stacks.
预印本.
(arXiv)Bu, C., Halpern-Leistner, D., Ibáñez Núñez, A., and Kinjo, T. Intrinsic Donaldson–Thomas theory. I. Component lattices of stacks.
预印本.
(arXiv)Bu, C., Pădurariu, T., and Toda, Y. Semiorthogonal decompositions for stacks.
进行中.